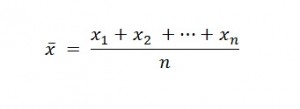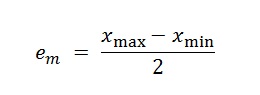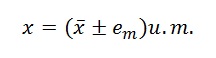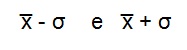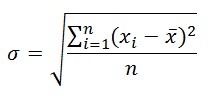Lezione 2: errori di misura

Lezione 2: errori di misura – Ogni qual volta si misura una grandezza fisica possono occorrere diversi tipi di errori.

• Errori sistematici: sono gli errori che si ripresentano in tutte le ripetizioni di una data misurazione, il più delle volte influiscono nello stesso senso (eccesso o difetto). Lo sperimentatore può ridurre questo errore se riesce ad individuarlo. Sono legati agli strumenti di misura o al metodo di misurazione.
• Errori accidentali: sono errori che si presentano in ciascuna misurazione in modo imprevedibile e possono influire sul risultato della misura in tutte e due i sensi (eccesso o difetto). Spesso sono dovuti all’imperfezione degli strumenti di misura e dei sensi dello sperimentatore.

 
Se gli errori sistematici possono essere ridotti adottando metodi di misurazione e strumenti più precisi, gli errori accidentali sono imprevedibile e l’unico rimedio è ripetere più e più volte l’esperimento in modo da stimare la grandezza degli errori.

Se ripetiamo n volte l’esperimento il valore che daremo alla grandezza (x) misurata sarà pari alla media dei valori ottenuti cioè:

 (1)

Si definisce poi l’errore massimo o assoluto come:

(2)

 

dove x_max e x_min sono rispettivamente il valore più grande ottenuto e il valore minimo.

La misura si rappresenta così:

 

 

dove u.m. sta per unità di misura.

 

Facciamo un esempio: supponiamo di aver misurato la durata t di 10 oscillazioni di un pendolo ottenendo i seguenti valori.

24,56 s

24,85 s

24,45 s

24,51 s

24,63 s

 

Applicando la formula (1) avremo che

mentre l’errore massimo, applicando la formula (2), sarà uguale a

e_max = 0,2 s

Esprimeremo la nostra misura del tempo come    t = (24,6±0,2) s

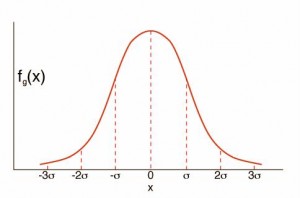
Quando il numero delle misure diventa consistente, se mettiamo in un grafico sulle ordinate la frequenza della misura, ovvero quante volte occorre un certo valore, e sulle ascisse i valori della misura avremo la curva di Gauss.

Per questa curva si è dimostrato che esiste una quantità, chiamata scarto quadratico medio o deviazione standard (σ), che ha una proprietà molto importante, infatti il 68,3% delle misure cadono all’interno dell’intervallo

 

La deviazione standard è data dalla formula:

 

 
dove x_i rappresenta la i-esima misura eè il valore medio ottenuto dalle misure stesse ed n è il numero delle misure effettuate.
Quindi il risultato di una grandezza x si esprime mediante il valor medio e lo scarto quadratico medio o deviazione standard σ.

 Da qui possiamo anche ricavare le cifre significative per una misura, ovvero le cifre certe più la prima incerta. Che cosa significa? Con un esempio capiremo meglio.

Supponete di aver misurato più volte il peso di un determinato oggetto e di aver determinato il suo valore medio e la deviazione standard:

 

La deviazione standard ci dice che si ha un’incertezza o un errore alla terza cifra decimale, quindi sarebbe inopportuno riportare tutte le cifre decimali del valore medio in quanto già dalla terza cifra decimale sarà affetta da incertezza, quindi il giusto modo di riportare la misura sarà:

 

 

Se volete essere sempre aggiornati su tutto ciò che concerne il blog basta un “mi piace” alla fanpage. Vi aspetto numerosi!

[banner]