Lezione 2: gli orbitali atomici

Lezione 2: gli orbitali atomici.

Come già detto nella lezione 1 gli orbitali atomici rappresentano, molto semplicisticamente, i risultati finali dell’equazione d’onda di Schrödinger e sono la rappresentazione grafica dello spazio in cui si ha la probabilità del 90% di trovare un determinato elettrone. La funzione d’onda orbitale, o orbitale, ci permette di descrivere lo stato quantico dell’elettrone ovvero la sua energia e la sua localizzazione nello spazio.

Lo stato energetico, la forma e l’orientamento nello spazio degli orbitali è definito da una serie di numeri chiamati numeri quantici: n, l, m ed m_s.

• Il primo numero quantico n, detto anche principale, determina l’energia dell’orbitale e può assumere solo valori interi positivi, quindi 1, 2, 3 etc. All’aumentare di n aumenta l’energia dell’orbitale e la sua distanza dal nucleo. Ciò significa che l’energia non può assumere qualsiasi valore ma solo quelli definiti da n,quindi si parla di l’energia quantizzata.
• Il secondo numero quantico l, detto azimutale, definisce la forma dell’orbitale. E’ legato al numero quantico principale n in quanto può assumere tutti i valori compresi tra 0 e n-1. I diversi valori che l può assumere non sono altro che il numero dei sottolivelli possibili per i vari livelli, e sono indicati con le lettere s, p, d, f (dopo di questi si prosegue in ordine alfabetico g, h etc) per ricordare la terminologia usata dagli spettroscopisti per distinguere le righe spettrali: sottile, principale, diffusa, fondamentale.
• Il terzo numero quantico m, detto magnetico, stabilisce l’orientazione nello spazio dell’obritale. È collegato a l in quanto può assumere tutti i valori compresi tra –l e +l; stabilisce anche quanti orbitari spettano ai singoli livelli.
• Il quarto numero quantico m_s, detto di spin, attribuisce all’elettrone un momento angolare intrinseco e può assumere soltanto due valori +1/2 e -1/2.

Il numero degli orbitali possibili è uguale a n² mentre il numero degli elettroni che si possono trovare in ogni livello è uguale a 2n².

E’ bene specificare che in ogni orbitale possono trovarsi al massimo due elettroni che avranno gli stessi numeri quantici tranne che per quello di spin; un elettrone avrà m_s = +1/2 e l’altro m_s = -1/2

Gli elettroni che occupano lo stesso orbitale sono necessariamente molto vicini e la loro coabitazione è possibile proprio perché hanno spin opposto.

Immaginateli come due piccoli magneti: se i poli sono opposti si attraggono se sono uguali si respingono, così gli spin.

 

A questo punto un esempio è d’uopo.

Se n=1 avremo che gli orbitali possibili saranno pari a n² = 1, quindi un solo orbitale. Gli elettroni saranno 2n² = 2

Sappiamo che 0< l < n-1

In questo caso dato che n = 1          

l =0 quindi avremo un unico sottolivello chiamato 1s

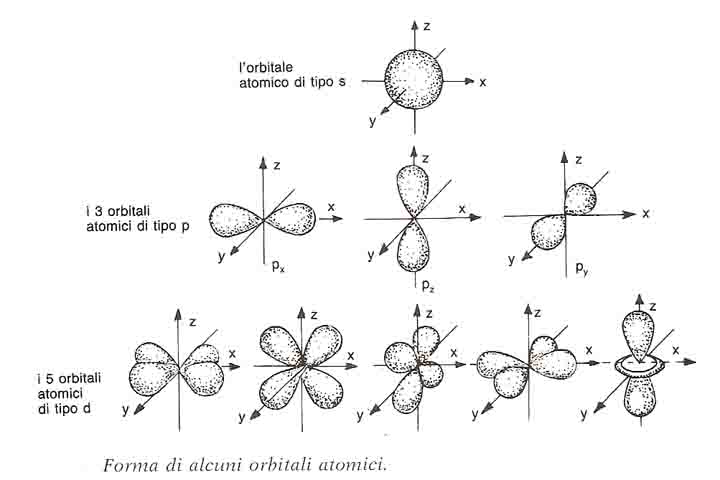
Sappiamo inoltre che  –l < m < +l    ma    l = 0    quindi anche     m = 0   pertanto il sottolivello s sarà formato da un unico orbitale (di forma sferica ad una distanza ben precisa dal nucleo, vedi immagine).

I due elettroni si troveranno all’interno dell’orbitale 1s con spin opposto.

 

Un altro esempio un po’ più complicato; al secondo livello energetico n = 2

n° orbitali possibili = n² = 4

n° elettroni =2n² = 8

l = 0, 1

Per cui al secondo livello energetico avremo:

-un sottolivello s, con un unico orbitale chiamato 2s, quando l = 0 ed m = 0

-un sottolivello p, con tre orbitali chiamati 2p quando l = 1 ed m = -1, 0,+1.

Gli orbitali 2p si dicono degeneri perché differiscono solo per il terzo numero quantico e sono sistemati su assi spaziali diversi (p_x, p_y,p_z vedi immagine).In ognuno di questi orbitali si troveranno due elettroni con spin opposto per un totale di 8.

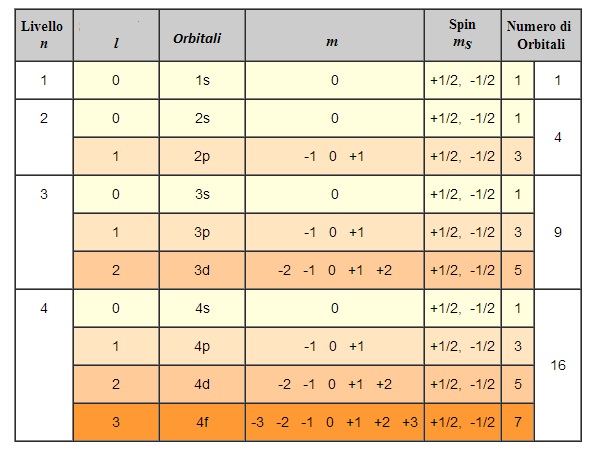
La tabella seguente mostrerà gli orbitali possibili per i vari livelli energetici.

 

 

Se volete essere sempre aggiornati su tutto ciò che concerne il blog basta un “mi piace” alla fanpage. Vi aspetto numerosi!

 [banner]

immagine: http://www.marconi-galletti.it